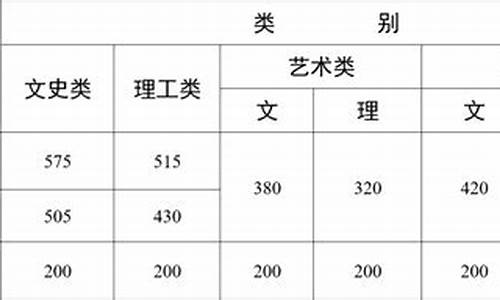
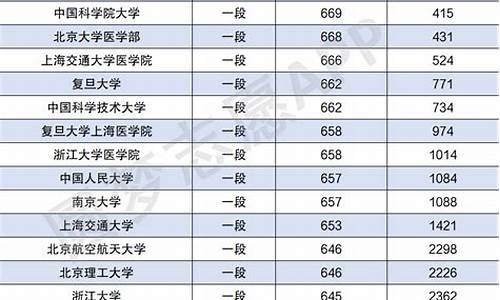
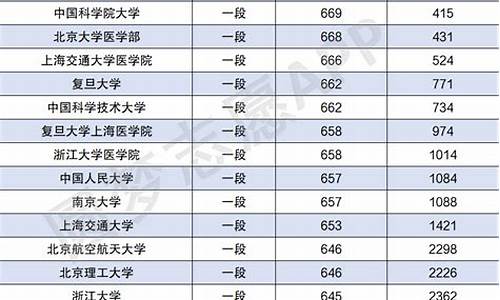
广东高考理科试卷及答案-2021广东高考理数

1.2016年广东高考用全国卷了.我是理科生.该怎样复习

2.数列{An}的前n项和为Sn,满足Sn=2nAn+1-3n^2-4n，n属于N*,14年广东高考理科19题有木有大神在啊 求解答

3.广东高考化学生物理科数学选择题一般考什么类型

4.2011广东高考数学试卷理科的最后一道大题是考什么知识点的

5.今年广东高考理科数学第十题答案是多少?网上查不到.

2016年广东高考用全国卷了.我是理科生.该怎样复习

你好，我是今年刚毕业的广东考生，首先你要把心态放平，不要害怕全国卷，全国卷确实比广东卷的难度有所加深，但考查的内容实际上是差不多的，可能全国卷与广东卷的题型不太一样，这是你需要关注的，复习最好跟着老师走，合理制定计划，可以自己买一本五三或者金考卷来做。

希望能帮助到你，请采纳哈，不懂可以再追问

数列{An}的前n项和为Sn,满足Sn=2nAn+1-3n^2-4n，n属于N*,14年广东高考理科19题有木有大神在啊 求解答

广东省2014年高考理科数学第19题答案如下：

（1）首先，由Sn的公式可以很容易的求出a1，因为S1=a1，带入到式子中，a1=2a2-7，同时，将n=2代入式子，则S2=a1+a2=4（15-a1-a2）-20，则a1+a2=8，将两式子联立，得a1=3，a2=5，因S3=15，故a3=7，所以a1=3、a2=5、a3=7。以上是第一问的标准解法。

（2）第二问是本题的难点，在解决数列问题时，有很多公式和技巧可以使用，本题则应用了最为普遍的解法：Sn-Sn-1=an，同样地，S（n+1）-Sn=a（n+1），将n+1和n代入Sn的通项公式中，得到如下图的公式：

很显然的，这个式子不是我们需要的通项公式，接下来我们就要利用其他条件了，观察第一问，根据a1=3、a2=5、a3=7，我们不难猜想，an=2n+1，但是猜想终归是猜想，我们需要进行证明，证明采用一种比较常规的证明方法：数学归纳法。

我们分为两种情况进行证明：①当n=1时，代入上面的式子（将中的式子命名为式子a）中，发现式子a符合2n+1这个式子，即证明当n=1时，确实满足an=2n+1。

②仅证明n=1是不可以的，我们需要证明当n=k（k属于n*时）仍然符合式子a，首先我们假设，n=k符合，然后证明n=k+1符合即可，假设n=k符合，则an=2k+1，那么这就是已知条件了，代入式子a，很容易导出，a（k+1）=2k+3=2（k+1）+1，假设n=k符合式子a，证明了n=k+1符合式子a，也就证明了an=2n+1是通项公式，本题作答结束。

本题运用的难点思想就是，需要假设n=k成立，然后证明n=k+1成立，可以这样想，当这个式子不断往后加1都是成立的，就说明这个式子不是只在某一部分符合，就像我们已知了a1、a2，a3，那么证明a4成立，然后已知a4成立，再证明a5成立，这样无穷尽的证明，发现只要k成立，k+1就成立，那么这个式子就是一个符合要求的通项公式。

广东高考化学生物理科数学选择题一般考什么类型

自己看下应该就明白了，题目大概都是这样子的，不太难，但是比较基础。

2011届高三第三次调研考试理科综合试题（2011.1） 一、单项选择题： 1．诗文“落红不是无情物，化作春泥更护花”中所蕴含的生命科学知识是 A．自然界的物质循环 B．生态系统恢复力稳定性强 C．生物的变异现象 D．生物的种间斗争关系 2．下列酶与其作用对应正确的是 A．纤维素酶——原生质体 B．限制酶——任何磷酸二酯键 C．解旋酶——碱基间氢键 D．ATP水解酶——肽键? 3．新物种形成的标志是 A. 具有一定的形态结构和生理功能 B. 产生了地理隔离 C. 形成了生殖隔离 D. 改变了基因频率 4．超级病菌是一种耐药性细菌，它最可能由普通细菌通过哪种变异形成 A．基因重组 B．染色体结构变异 C．基因突变 D．染色体数目变异 5．孟德尔对分离现象的原因提出了假说，下列不属于该假说内容的是 A．生物的性状是由遗传因子决定的 B．基因在体细胞染色体上成对存在 C．配子只含有每对遗传因子中的一个 D．受精时雌雄配子的结合是随机的

13?在同一点O抛出的三个物体?做平抛运动的轨迹如图所示?则三个物体做平抛运动的初速度vA、vB、vC的关系和三个物体做平抛运动的时间tA、tB、tC的关系分别是? ? A.vA?vB?vC?tA?tB?tC B.vA?vB?vC?tA?tB?tC C.vA?vB?vC?tA?tB?tC D.vA?vB?vC?tA?tB?tC 14?下列说法中正确的是 ? ? A.布朗运动是用显微镜观察到的分子的运动 B.由于气体分子之间存在斥力作用?所以压缩气体时会感到费力 C.若气体的体积增大?则气体对外做功?但气体的内能有可能保持不变 D.热量可能自发地从低温物体传递到高温物体. 15.如图所示?A、B为相同的两个灯泡?均发光?当变阻器的滑片P向下端滑动时?则 A?A灯变亮?B灯变暗 B?A灯变暗?B灯变亮 C?A、B灯均变亮 D?A、B灯均变暗 16?下列说法中正确的是 ? ? A. 物体的温度升高?物体所含的热量就增多 B. 物体的温度不变?内能一定不变 C. 热量和功的单位与内能的单位相同?所以热量和功都作为物体内能的量度 D. 热量和功是由过程决定的?而内能是由物体的状态决定的. 17?如图所示?一带负电粒子以某速度进入水平向右的匀强电场中?在电场力作用下形成图中所示的运动轨迹。M和N是轨迹上的两点?其中M点在轨迹的最右点。不计重力?下列表述正确的是? ? A?粒子在M点的速率最小 B?粒子所受电场力沿电场方向 C?粒子在电场中的加速度不变 D?粒子在电场中的电势能始终在增加 18?如图所示?a为放在赤道上的物体?b为沿地球表面附近做匀圆周运动的人造卫星?c为地球同步卫星。以下关于a、b、c的说法中正确的是 ? ? A.a、b、c作为匀速圆周运动的向心加速度大小关系为aa?ab?ac B.a、b、c作为匀速圆周运动的向心加速度大小关系为ab?ac?aa C.a、b、c作为匀速圆周运动的线速度大小关系为va=vb?vc D.a、b、c作为匀速圆周运动的周期关系为Ta=Tc?Tb. 19?如右图所示?A、B两物体质量分别为mA=5kg和mB=4kg?与水平地面

2011年高考广东卷 理科综合理科综合理科综合理科综合A卷卷卷卷化学化学化学化学参考答案参考答案参考答案参考答案 一、单选题 7. 下列说法正确的是 A.纤维素和淀粉遇碘水均显蓝色 B.蛋白质、乙酸和葡萄糖均属电解质 C.溴乙烷与NaOH乙醇溶液共热生成乙烯 D.乙酸乙酯和食用植物油均可水解生成乙醇 解析：A.纤维素遇碘水不能显蓝色B.蛋白质，葡萄糖不是电解质D, 食用植物油水解有甘油生成 8. 能在水溶液中大量共存的一组离子是 A. H＋、I―、NO3―、SiO32－ B. Ag＋、Fe3＋、Cl―、SO42― C.K＋、SO42－、Cu2＋、NO3― D.NH4＋、OH－、Cl－、HCO3－ 解析：A. H＋、I―、NO3―、三者发生氧化还原反应；H＋，SiO32－ 生成沉淀 。 B. Ag＋与Cl―、SO42―形成沉淀。D.NH4＋与OH－和OH－与HCO3－均反应 9.设nA为阿伏伽德罗常数的数值，下列说法正确的是 A、常温下，23g NO2含有nA个氧原子 B、1L0.1mol?L-1的氨水含有0.1nA个OH― C、常温常压下，22.4LCCl4含有个nACCl4分子 D、1molFe2+与足量的H2O2溶液反应，转移2nA个电子[来源:学科网] 解析：B、弱电解质部分电离，小于0.1nA个。C、条件和状态不对。D、1molFe2+作还原剂，转移nA个电子 10、某同学通过系列实验探究Mg及其化合物的性质，操作正确且能达到目的的是 A、将水加入浓硫酸中得到稀硫酸，置镁条于其中探究Mg的活泼性 B、将NaOH溶液缓慢滴入MgSO4溶液中，观察Mg(OH)2沉淀的生成 C、将Mg(OH)2浊液直接倒入已装好滤纸的漏斗中过滤，洗涤并收集沉淀 D、将Mg(OH)2沉淀转入蒸发皿中，加足量稀盐酸

2011广东高考数学试卷理科的最后一道大题是考什么知识点的

该题考查主要是解析几何里面的内容，主要考察抛物线与直线的关系，但该题又考查了用导数求切线方程，利用直线点斜式求切线方程，利用了不等式的性质，抛物线的性质，函数求最值的方法，直线斜率公式，二次方程的有关内容等。

今年广东高考理科数学第十题答案是多少?网上查不到.

2009年广东高考数学理科试题和答案(答案已更新)

2009-6-15 10:36:00

2009年普通高等学校招生全国统一考试（广东卷）

数学（理科）参考答案

一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 已知全集 ，集合 和 的关系的韦恩（Venn）图如图1所示，则阴影部分所示的集合的元素共有

A. 3个 B. 2个

C. 1个 D. 无穷多个

解析由 得 ，则 ，有2个，选B.

2. 设 是复数， 表示满足 的最小正整数 ，则对虚数单位 ，

A. 8 B. 6 C. 4 D. 2

解析 ，则最小正整数 为4，选C.

3. 若函数 是函数 的反函数，其图像经过点 ，则

A. B. C. D.

解析 ，代入 ，解得 ，所以 ，选B.

4.已知等比数列 满足 ，且 ，则当 时，

A. B. C. D.

解析由 得 ， ，则 ， ，选C

5. 给定下列四个命题：

①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；

②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；

③垂直于同一直线的两条直线相互平行；

④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．

其中，为真命题的是

A. ①和② B. ②和③ C. ③和④ D. ②和④

解析选D.

6. 一质点受到平面上的三个力 （单位：牛顿）的作用而处于平衡状态．已知 ， 成 角，且 ， 的大小分别为2和4，则 的大小为

A. 6 B. 2 C. D.

解析 ，所以 ，选D.

7．2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张和小赵只能从事前两项工作，其余三人均能从事这四项工作，则不同的选派方案共有

A. 36种 B. 12种 C. 18种 D. 48种

解析分两类：若小张或小赵入选，则有选法 ；若小张、小赵都入选，则有选法 ，共有选法36种，选A

8．已知甲、乙两车由同一起点同时出发,并沿同一路线（假定为直线）行驶．甲车、乙车的速度曲线分别为 （如图2所示）．那么对于图中给定的 ，下列判断中一定正确的是

A. 在 时刻，甲车在乙车前面

B. 时刻后，甲车在乙车后面

C. 在 时刻，两车的位置相同

D. 时刻后，乙车在甲车前面

解析由图像可知，曲线 比 在0～ 、0～ 与 轴所围成图形面积大，则在 、 时刻，甲车均在乙车前面，选A

二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．

（一）必做题（9 ~ 12题）

9. 随机抽取某产品 件，测得其长度分别为 ，则图3所示的程序框图输出的 ， 表示的样本的数字特征是 ．（注：框图中的赋值符号“=”也可以写成“←”“：=”）

解析 ；平均数

10. 若平面向量 ， 满足 ， 平行于 轴， ，则

解析 或 ，则 或 .

11．巳知椭圆 的中心在坐标原点，长轴在 轴上，离心率为 ，且 上一点到 的两个焦点的距离之和为12，则椭圆 的方程为 ．

解析 ， ， ， ，则所求椭圆方程为 .

12．已知离散型随机变量 的分布列如右表．若 ， ，则 ， ．

解析由题知 ， ， ，解得 ， .

（二）选做题（13 ~ 15题，考生只能从中选做两题）

13．（坐标系与参数方程选做题）若直线 （ 为参数）与直线 （ 为参数）垂直，则 ．

解析 ，得 .

14．（不等式选讲选做题）不等式 的实数解为 ．

解析 且 .

15．（几何证明选讲选做题）如图4，点 是圆 上的点， 且 ， 则圆 的面积等于 ．

解析解法一：连结 、 ，则 ，∵ ， ，∴ ，则 ；解法二： ，则 .

三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤.

16．(本小题满分12分）

已知向量 与 互相垂直，其中 ．

（1）求 和 的值；

（2）若 ，求 的值．

解：（1）∵ 与 互相垂直，则 ，即 ，代入 得 ，又 ，∴ .

（2）∵ ， ，∴ ，则 ，∴ .

17．（本小题满分12分）

根据空气质量指数API（为整数）的不同，可将空气质量分级如下表：

对某城市一年（365天）的空气质量进行监测，获得的API数据按照区间 ， ， ， ， ， 进行分组，得到频率分布直方图如图5.

（1）求直方图中 的值；

（2）计算一年中空气质量分别为良和轻微污染的天数；

（3）求该城市某一周至少有2天的空气质量为良或轻微污染的概率.

（结果用分数表示．已知 ， ， ， ）

解：（1）由图可知 ，解得 ；

（2） ；

（3）该城市一年中每天空气质量为良或轻微污染的概率为 ，则空气质量不为良且不为轻微污染的概率为 ，一周至少有两天空气质量为良或轻微污染的概率为 .

18．（本小题满分14分）

如图6，已知正方体 的棱长为2，点 是正方形 的中心，点 、 分别是棱 的中点．设点 分别是点 ， 在平面 内的正投影．

（1）求以 为顶点，以四边形 在平面 内的正投影为底面边界的棱锥的体积；

（2）证明：直线 平面 ；

（3）求异面直线 所成角的正弦值.

解：（1）依题作点 、 在平面 内的正投影 、 ，则 、 分别为 、 的中点，连结 、 、 、 ，则所求为四棱锥 的体积，其底面 面积为

，

又 面 ， ，∴ .

（2）以 为坐标原点， 、 、 所在直线分别作 轴， 轴， 轴，得 、 ，又 ， ， ，则 ， ， ，

∴ ， ，即 ， ，

又 ，∴ 平面 .

（3） ， ，则 ，设异面直线 所成角为 ，则 .

19．（本小题满分14分）

已知曲线 与直线 交于两点 和 ，且 ．记曲线 在点 和点 之间那一段 与线段 所围成的平面区域（含边界）为 ．设点 是 上的任一点，且点 与点 和点 均不重合．

（1）若点 是线段 的中点，试求线段 的中点 的轨迹方程；

（2）若曲线 与 有公共点，试求 的最小值．

解：（1）联立 与 得 ，则 中点 ，设线段 的中点 坐标为 ，则 ，即 ，又点 在曲线 上，

∴ 化简可得 ，又点 是 上的任一点，且不与点 和点 重合，则 ，即 ，∴中点 的轨迹方程为 （ ）.

（2）曲线 ，

即圆 ： ，其圆心坐标为 ，半径

由图可知，当 时，曲线 与点 有公共点；

当 时，要使曲线 与点 有公共点，只需圆心 到直线 的距离 ，得 ，则 的最小值为 .

20．（本小题满分14分）

已知二次函数 的导函数的图像与直线 平行，且 在 处取得极小值 ．设 ．

（1）若曲线 上的点 到点 的距离的最小值为 ，求 的值；

（2） 如何取值时，函数 存在零点，并求出零点．

解：（1）依题可设 ( )，则 ；

又 的图像与直线 平行

， ，

设 ，则

当且仅当 时， 取得最小值，即 取得最小值

当 时， 解得

当 时， 解得

（2）由 ( )，得

当 时，方程 有一解 ，函数 有一零点 ；

当 时，方程 有二解 ，

若 ， ，

函数 有两个零点 ，即 ；

若 ， ，

函数 有两个零点 ，即 ；

当 时，方程 有一解 , ,

函数 有一零点

综上，当 时, 函数 有一零点 ；

当 ( )，或 （ ）时，

函数 有两个零点 ；

当 时，函数 有一零点 .

21．（本小题满分14分）

已知曲线 ．从点 向曲线 引斜率为 的切线 ，切点为 ．

（1）求数列 的通项公式；

（2）证明： .

解：（1）设直线 ： ，联立 得 ，则 ，∴ （ 舍去）

，即 ，∴

（2）证明：∵

∴

由于 ，可令函数 ，则 ，令 ，得 ，给定区间 ，则有 ，则函数 在 上单调递减，∴ ，即 在 恒成立，又 ，

则有 ，即