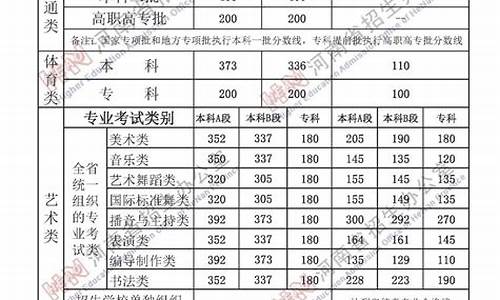
20217高考数学,20l7年高考数学

1.2017年数学高考考纲和16年的区别

2.贵州17年高考数学难度大吗

3.2017年高考数学文化指什么

LZ您好

全国卷2本来就不是难卷,且2017年的全国卷2的难度"歪了"

歪的地方是题目不算新,计算量挺大(第18题概率论与数理统计的大题,并且位置靠前,后面大题不难但是做完这题心态容易崩)

所以有一定计算量训练的学生这张卷应该很轻松

基础选择填空完全在比简单题用时...

可能拉分的题:

选择题最后一题建立坐标系进行向量计算,立刻天就蓝了...结果还是考计算量!

填空倒数第二题是裂项

填空最后一题画完图结果还是变成计算题...

三角大题是基础.

圆锥曲线和立体几何大题也是思路送分,看你认不认真计算.

压轴导数题算不得难但是(1)须有极限思想;(2)是分类讨论,存在唯一极大值点被你证明好了这题也结束了.

坐标系与参数方程选修题有积化和差的技巧...不等式的那个选修题也是套路,但是是证明题,所以难度比坐标系题要难...

所以这张卷子,真心难度不大,问做题认真不认真,计算量稍微偏大而已.

2017年数学高考考纲和16年的区别

121.13分。根据江苏教育局官网查询得知，2017年江苏高考各科平均分如下：语文：113.99分，数学：121.13分，英语：112.32分，物理：87.92分，化学：100.91分，生物：94.32分。2017江苏省高考各科总分，只计语文、数学、外语三科，其中普通文、理科总分480分，文科生语文200分，数学160分，外语120分；理科生语文160分，数学200分，外语120分。

贵州17年高考数学难度大吗

1、增加了数学文化的要求。

2、在能力要求内涵方面，增加了基础性、综合性、应用性、创新性的要求，同时对能力要求进行了加细说明，使能力要求更加明确具体。

3、在现行考试大纲三个选考模块中删去《几何证明选讲》，其余2个选考模块的内容和范围都不变，考生从《坐标系与参数方程》、《不等式选讲》2个模块中任选1个作答。

总体上，这些变化对2017年高考数学考试影响不大。基于两个原因：

一是在这次高考考纲修订基本原则 “坚持整体稳定，推进改革创新；优化考试内容，着力提高质量；提前谋篇布局，体现素养导向”中，将“整体稳定”放在了首位。2015年、2016年全国数学2卷就突出了稳中求变，约有80%的试题是稳定的，只有约20%的试题是创新的，2017年高考仍然还会沿用这种思路命制试卷。

二是近两年高考试卷已先于2017年高考考纲在命题中渗透了一些变化与创新，全国数学2卷最大的变化点是，突出了社会主义核心价值观，强调了中国传统数学文化精髓。在数学文化方面，2016年高考全国2卷理科数学第8题、文科数学第9题涉及到了我国南宋著名数学家秦九韶提出的多项式求值的算法，2015年高考全国2卷文、理科数学的第8题涉及到了我国古代数学名著《九章算术》中的“更相减损术”。

这就是说，今年考纲中所提到的新要求、新变化，在两年前的高考中就已经有所体现了，所以2017年高考对我们而言变化不会很大。而第三项变化是选考题由“三选一”变为“二选一”，这将减轻学生的课业负担。

2017年高考数学文化指什么

不大。根据查询贵州教育局官网得知，2017年贵州省普通高考数学题难度不大，没有偏难怪题，区分度较好，试卷所考查的知识和能力符合考试大纲的内容和要求。普通高等学校招生全国统一考试简称高考，是中华人民共和国合格的高中毕业生或具有同等学力的考生参加的选拔性考试。

在即将公布的高中数学课程标准中，数学文化是一个单独的板块，给予了特别的重视。许多老师会问为什么要这样做？一个重要的原因是，20世纪初年的数学曾经存在着脱离社会文化的孤立主义倾向，并一直影响到今天的中国。数学的过度形式化，使人错误地感到数学只是少数天才脑子里想象出来的“自由创造物”，数学的发展无须社会的推动，其真理性无须实践的检验，当然，数学的进步也无须人类文化的哺育。于是，西方的数学界有“经验主义的复兴”。怀特（White）的数学文化论力图把数学回归到文化层面。克莱因（Kline）的《古今数学思想》、《西方文化中的数学》、《数学：确定性的丧失》相继问世，力图营造数学文化的人文色彩。

国内最早注意数学文化的学者是北京大学的教授孙小礼，她和邓东皋等合编的《数学与文化》，汇集了一些数学名家的有关论述，也记录了从自然辩证法研究的角度对数学文化的思考。稍后出版的有齐民友的《数学与文化》，主要从非欧几何产生的历史阐述数学的文化价值，特别指出了数学思维的文化意义。郑毓信等出版的专著《数学文化学》，特点是用社会建构主义的哲学观，强调“数学共同体”产生的文化效应。

以上的著作以及许多的论文，都力图把数学从单纯的逻辑演绎推理的圈子中解放出来，重点是分析数学文明史，充分揭示数学的文化内涵，肯定数学作为文化存在的价值。

进入21世纪之后，数学文化的研究更加深入。一个重要的标志是数学文化走进中小学课堂，渗入实际数学教学，努力使学生在学习数学过程中真正受到文化感染，产生文化共鸣，体会数学的文化品位，体察社会文化和数学文化之间的互动。

那么，如何在中小学数学教学中进行数学文化教育呢？笔者认为应该从以下几个方面加以认识和实施。

每个民族都有自己的文化，也就一定有属于这个文化的数学。古希腊的数学和中国传统数学都有辉煌的成就、优秀的传统。但是，它们之间有着明显的差异。古希腊和古代中国的不同政治文明孕育了不同的数学。

古希腊是奴隶制国家。当时希腊的雅典城邦实行奴隶主的民主政治（广大奴隶不能享受这种民主）。男性奴隶主的全体大会选举执政官，对一些战争、财政大事实行民主表决。这种政治文明包含着某些合理的因素。奴隶主之间讲民主，往往需要用理由说服对方，使学术上的辩论风气浓厚。为了证明自己坚持的是真理，也就需要证明。先设一些人人皆同意的“公理”，规定一些名词的意义，然后把要陈述的命题，称为公理的逻辑推论。欧氏的《几何原本》正是在这样的背景下产生的。

中国在春秋战国时期也有百家争鸣的学术风气，但是没有实行古希腊统治者之间的民主政治，而是实行君王统治制度。春秋战国时期，也是知识分子自由表达见解的黄金年代。当时的思想家和数学家，主要目标是帮助君王统治臣民、管理国家。因此，中国的古代数学，多半以“管理数学”的形式出现，目的是为了丈量田亩、兴修水利、分配劳力、计算税收、运输粮食等国家管理的实用目标。理性探讨在这里退居其次。因此，从文化意义上看，中国数学可以说是“管理数学”和“木匠数学”，存在的形式则是官方的文书。

古希腊的文化时尚，是追求精神上享受，以获得对大自然的理解为最高目标。因此，“对顶角相等”这样的命题，在《几何原本》里列入命题15，借助公理3（等量减等量，其差相等）给予证明。在中国的数学文化里，不可能给这样的直观命题留下位置。

同样，中国数学强调实用的管理数学，却在算法上得到了长足的发展。负数的运用、解方程的开根法，以及杨辉（贾宪）三角、祖冲之的圆周率计算、天元术那样的精致计算课题，也只能在中国诞生，而为古希腊文明所轻视。

我们应当充分重视中国传统数学中的实用与算法的传统，同时又必须吸收人类一切有益的数学文化创造，包括古希腊的文化传统。当进入21世纪的时候，我们作为地球村的村民，一定要溶入世界数学文化，将民族性和世界性有机地结合起来。