14年高考线-2014高考切线

1.高考数学证明：”证明：过抛物线准线上的点做抛物线两条切线，则两个切点所在直线过焦点。

2.有没有会解下面这道高考题的，四川省2014年高考理科数学第19题。求大神解答~~题目如下，关于数列的

3.高考切线的有点不懂

4.福建省近三年高考切线

5.2014江西数学数学高考试卷 数学很难？

高考数学证明：”证明：过抛物线准线上的点做抛物线两条切线，则两个切点所在直线过焦点。

证明：不妨设抛物线是x^2=4py(p>0),准线是y=-p,焦点F(0,p)

设M(t,-p)是准线上任意一点,过M作抛物线的两条切线MA、MB,A、B是切点。

因A、B在抛物线上，设A(2pm,pm^2),B(2pn,pn^2) (m≠n)

由x^2=4py 得y=x^2/(4p), y'=x/(2p)

在A处切线斜率k=m，切线方程是mx-y-pm^2=0

它过M(t,-p)得 mt+p-pm^2=0

即 pm^2-tm-p=0 (1)

在B处切线斜率k=n，切线方程是nx-y-pn^2=0

它过M(t,-p)得 nt+p-pn^2=0

即 pn^2-tn-p=0 (2)

由(1)(2) 得m，n是方程z^2-tz-p=0的两个根

得 m+n=t/p，且 mn=-1 (3)

由A(2pm,pm^2)，B(2pn,pn^2) (m≠n)可得直线AB的方程是

(m+n)x-2y-2pmn=0

将(3)代入得 (t/p)x-2y+2p=0

即 tx-2p(y-p)=0

该直线恒过F(0,p)?

得证。

扩展资料：

抛物线的一个描述涉及一个点（焦点）和一条线（准线）。焦点并不在准线上。抛物线是该平面中与准线和焦点等距的点的轨迹。抛物线的另一个描述是作为圆锥截面，由圆锥形表面和平行于锥形母线的平面的交点形成。第三个描述是代数。

抛物线具有这样的性质，如果它们由反射光的材料制成，则平行于抛物线的对称轴行进并撞击其凹面的光被反射到其焦点，而不管抛物线在哪里发生反射。相反，从焦点处的点源产生的光被反射成平行（“准直”）光束，使抛物线平行于对称轴。声音和其他形式的能量也会产生相同的效果。这种反射性质是抛物线的许多实际应用的基础。

百度百科-抛物线

有没有会解下面这道高考题的，四川省2014年高考理科数学第19题。求大神解答~~题目如下，关于数列的

这个题综合考查了指数函数的运算性质,导数的几何意义,等差数列与等比数列的通项公式及其前n项和公式等基础知识与基本技能方法,考查了推理能力,计算能力,"错位相减法",难度还是挺大的。不过答案在下面，仔细看下答案及解题思路，相信你就明白了~

这里就是答案://gz.qiujieda/exercise/math/804188等差数列{an}的公差为d，点（an，bn）在函数f（x）=2^x的图象上（n∈N*）．

（1）若a1=-2，点（a8，4b7）在函数f（x）的图象上，求数列{an}的前n项和Sn；

（2）若a1=1，函数f（x）的图象在点（a2，b2）处的切线在x轴上的截距为2-1/ln2,求数列{an/bn }的前n项和Tn

高考切线的有点不懂

1:11切线：意思是收一个人要公布前11人的分数。设有1100人参考，收10人，那么就要公布包括那10人在内的110人的分数，而那第110名的那人的分数就是切线分！

不晓得明白了没？

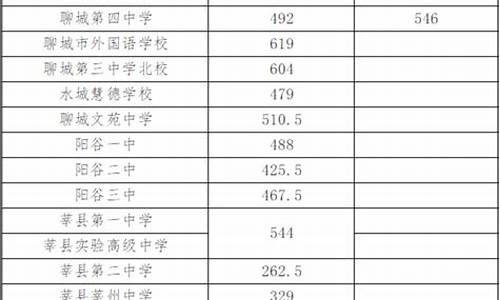
福建省近三年高考切线

福建省份近三年高考切线如下：

1、2022年高考批次线：

首选历史特招线：542分，首选物理特招线：520分。

首选历史本科线：468分，首选物理本科线：428分。

首选历史专科线：220分，首选物理专科线：220分。

2、2021年高考批次线：

首选历史特招线：546分，首选物理特招线：530分。

首选历史本科线：467分，首选物理本科线：423分。

首选历史专科线：220分，首选物理专科线：220分。

3、2020年高考批次线：

文科特招线：550分，理科特招线：516分。

文科本科线：465分，理科本科线：402分。

文科专科线：220分，理科专科线：220分。

福建的大学如下：

1、厦门大学

厦门大学（XiamenUniversity），简称厦大（XMU），由著名爱国华侨领袖陈嘉庚先生于1921年创办,是中国近代教育史上第一所华侨创办的大学。

2、福州大学

福州大学是国家“双一流”建设高校、国家“211工程”重点建设大学、福建省人民与国家教育部共建高校。学校创建于1958年，现已发展成为一所以工为主、理工结合，理、工、经、管、文、法、艺等多学科协调发展的重点大学。

3、福建师范大学

福建师范大学坐落于素有“海滨邹鲁”之誉的历史文化名城福州，是一所历史悠久、声誉斐然的百年省属高等学府。由华南女子文理学院、福建协和大学、福建省立师范专科学校等单位几经调整合并，于1953年成立福建师范学院，12年易名为福建师范大学并沿用至今。

以上数据出自《知乎》。

2014江西数学数学高考试卷 数学很难？

2014年普通高等学校招生全国统一考试（江西卷）

数学（理科）

一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 是的共轭复数. 若，（（为虚数单位），则（ ）

A. B. C. D.

2. 函数的定义域为（ ）

A. B. C. D.

3. 已知函数，，若，则（ ）

A. 1 B. 2 C. 3 D. -1

4.在中，内角A,B,C所对应的边分别为，若则的面积（ ）

A.3 B. C. D.

5.一几何体的直观图如右图，下列给出的四个俯视图中正确的是（ ）

6.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系，随机抽查52名中学生，得到统计数据如表1至表4，泽宇性别有关联的可能性最大的变量是（ ）

A.成绩 B.视力 C.智商 D.阅读量

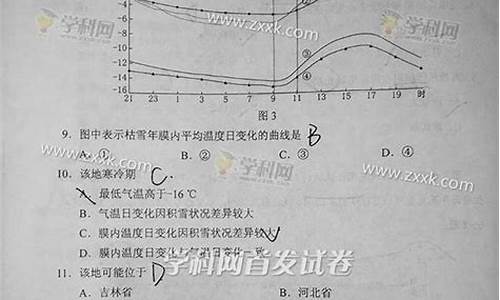
7.阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为（ ）

A.7 B.9 C.10 D.11

8.若则（ ）

A. B. C. D.1

9.在平面直角坐标系中，分别是轴和轴上的动点，若以为直径的圆与直线相切，则圆面积的最小值为（ ）

A. B. C. D.

10.如右图，在长方体中，=11，=7，=12，一质点从顶点A射向点，遇长方体的面反射（反射服从光的反射原理），将次到第次反射点之间的线段记为，，将线段竖直放置在同一水平线上，则大致的图形是（ ）

二.选做题：请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分，本题共5分.在每小题给出的四个选项中，只有一项是符合题目要求的.

11(1).（不等式选做题）对任意,的最小值为（ ）

A. B. C. D.

11(2).（坐标系与参数方程选做题）若以直角坐标系的原点为极点，轴的非负半轴为极轴建立极坐标系，则线段的极坐标为（ ）

A. B. C. D.

三.填空题：本大题共4小题，每小题5分，共20分.

12.10件产品中有7件正品，3件次品，从中任取4件，则恰好取到1件次品的概率是________.

13.若曲线上点处的切线平行于直线，则点的坐标是________.

14.已知单位向量与的夹角为，且，向量与的夹角为，则=

15.过点作斜率为的直线与椭圆：相交于，若是线段的中点，则椭圆的离心率为

三.简答题

16.已知函数，其中

（1）当时，求在区间上的最大值与最小值；

(2)若，求的值.

17、（本小题满分12分）

已知首项都是1的两个数列（），满足.

(1) 令，求数列的通项公式；

(2) 若，求数列的前n项和.

18、（本小题满分12分）

已知函数.

(1) 当时，求的极值；

(2) 若在区间上单调递增，求b的取值范围.

19(本小题满分12分)

如图，四棱锥中，为矩形，平面平面.

（1）求证：

（2）若问为何值时，四棱锥的体积最大？并求此时平面与平面夹角的余弦值.

20.（本小题满分13分）

如图，已知双曲线的右焦点,点分别在的两条渐近线上，轴，∥(为坐标原点）.

（1）求双曲线的方程；

（2）过上一点的直线与直线相交于点，与直线相交于点，证明点在上移动时，恒为定值，并求此定值

21.（满分14分）随机将这2n个连续正整数分成A,B两组，每组n个数，A组最小数为，最大数为；B组最小数为，最大数为，记

（1）当时，求的分布列和数学期望；

（2）令C表示与的取值恰好相等，求C发生的概率；

（3）对（2）中的C,表示C的对立，判断和的大小关系，并说明理由。