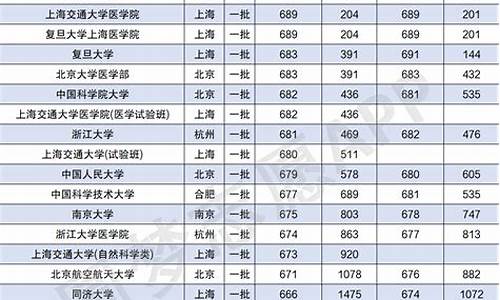
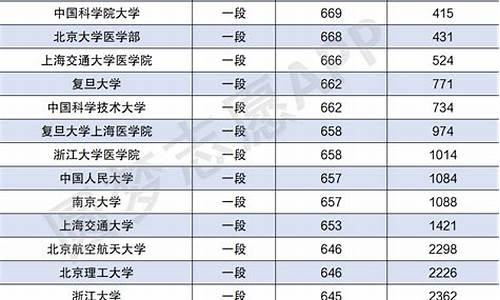
2017安徽高考数学理,2017安徽高考理科数学

1.2017年高考数学自主命题的省份有哪些

2.2017年高考数学必考等差数列公式

几何题复习最重要的就是要掌握好相应的高中数学面积以及体积公式，这样才能避免在高中数学几何题中丢分。接下来我为你整理了高中数学面积体积公式，一起来记一记吧。

高中数学面积体积公式1-5

　1、圆柱体:

　表面积:2?Rr+2?Rh

　体积:?R2h (R为圆柱体上下底圆半径,h为圆柱体高)

　2、圆锥体:

　表面积:?R2+?R[(h2+R2)的平方根]

　体积: ?R2h/3 (r为圆锥体低圆半径,h为其高,

　3、正方体

　a-边长， S=6a2 ，

　V=a3

　4、长方体

　a-长 ,b-宽 ,c-高 S=2(ab+ac+bc) V=abc

　5、棱柱 、 S-底面积 h-高

　V=Sh

高中数学面积体积公式6-10

　6、棱锥

　S-底面积 h-高

　V=Sh/3

　7、棱台

　S1和S2-上、下底面积 h-高

　V=h[S1+S2+(S1S2)^1/2]/3

　8、拟柱体

　S1-上底面积 ，S2-下底面积 ，S0-中截面积 h-高，

　V=h(S1+S2+4S0)/6

　9、圆柱

　r-底半径 ，h-高 ，C?底面周长 S底?底面积 ，S侧?侧面积 ，S表?表面积

　C=2?r

　S底=?r2，

　S侧=Ch ，

　S表=Ch+2S底 ，

　V=S底h=?r2h

　10、空心圆柱

　R-外圆半径 ，r-内圆半径 h-高

　V=?h(R^2-r^2)

高中数学面积体积公式11-17

　11、直圆锥 r-底半径 h-高

　V=?r^2h/3

　12、圆台

　r-上底半径 ，R-下底半径 ，h-高 V=?h(R2+Rr+r2)/3

　13、球

　r-半径 d-直径

　V=4/3?r^3=?d^3/6

　14、球缺

　h-球缺高，r-球半径，a-球缺底半径

　V=?h(3a2+h2)/6 =?h2(3r-h)/3

　15、球台

　r1和r2-球台上、下底半径 h-高

　V=?h[3(r12+r22)+h2]/6

　16、圆环体

　R-环体半径 D-环体直径 r-环体截面半径 d-环体截面直径

　V=2?2Rr2 =?2Dd2/4

　17、桶状体

　D-桶腹直径 d-桶底直径 h-桶高

　V=?h(2D2+d2)/12 ，(母线是圆弧形,圆心是桶的中心)

　V=?h(2D2+Dd+3d2/4)/15 (母线是抛物线形)

猜你喜欢：

1. 2017高考数学必考公式大全

2. 高中数学曲线公式

3. 高中数学知识点总结及公式大全

4. 2017年高考必备文科数学公式

5. 高中数学公式排列组合

6. 高中数学几何公式知识

2017年高考数学自主命题的省份有哪些

　2017年高考已经结束了，那么2017年高考总分多少分?各科的总分都是多少?下面是我整理的2017年各省高考总分，希望能给大家带来帮助!

　 2017年各省高考总分

　就全国的形式来讲，大部分地区的总分值还是一样的，如：安徽、北京、福建、甘肃、广东、广西、贵州、河北、河南、黑龙江、湖北、湖南、吉林、江西、辽宁、内蒙、宁夏、青海、山东、山西、陕西、四川、天津、西藏、新疆、云南、重庆等27个省市还是750分满分。各科的分值详情如下：语文150分，数学150分，英语150分，文综/理综300分。

　个别改革地区的分值详情需要大家做详细的了解，比如江苏、上海、浙江和海南这4个地区：

　浙江地区的高考总分：

　上海和浙江地区2017年采用的是3+3考试模式，即3门必考科目(语文、数学、英语)+选考科目，我们先来看浙江地区的总分：

　其中语文、数学和外语三科满分各为150分，其中英语笔试满分120分，英语听力考试满分30分;综合(文/理)满分300分;自选模块满分60分;技术满分100分，由通用技术和信息技术两科目成绩按各占50%的比例合成。

　需要特别提醒大家的是浙江的总分根据大家的选择而有所差异，即考生文化成绩总分按报考(含兼报)的不同考试类别分别合成。文理科一类为“3+综合+自选模块”的总分，满分为810分;二类为“3+综合”的总分，满分为750分;三类为“3+技术”的总分，满分为550分。

　上海地区的高考总分：

　2017年上海高考成绩满分660分，各科的分值详情是这样的哦：语文、数学(文/理)、外语满分均为150分，政治、历史、地理、物理、化学、生物任选3门：每门70分。

　 江苏地区的高考总分：　　

　江苏同样采用的是必考+选考模式，其中统考科目为语文、数学、外语三门，各科分值设定为：语文160分，数学160分，外语120分，共440分。语文、数学分别另设附加题40分，总分480分。

　选测科目各科满分为120分，按考生成绩分布分为A+、A、B+、B、C、D六个等级。

　 海南地区的高考总分：

　2017年海南的总分以900分的满分当之无愧的位据全国首位，语文、数学(文)、数学(理)、英语等科目的满分值均为150分，其中，英语科分听力和笔试两部分，笔试部分满分值为120分，听力部分满分值为30分，听力成绩计入英语科总分。政治、历史、地理、物理、化学、生物等科目的满分值均为100分，

2017年高考数学必考等差数列公式

全国Ⅰ卷地区：河南、河北、山西、江西、湖北、湖南、广东、安徽、福建

全国Ⅱ卷地区：甘肃、青海、内蒙古、黑龙江、吉林、辽宁、宁夏、新疆、西藏、陕西、重庆

全国Ⅲ卷地区：云南、广西、贵州、四川

海南省：全国Ⅱ卷(语、数、英)+单独命题(政、史、地、物、化、生)

山东省：全国Ⅰ卷(外语、文综、理综)+自主命题(语文、文数、理数)

江苏省：全部科目自主命题

北京市：全部科目自主命题

天津市：全部科目自主命题

　等差数列是常见数列的一种，如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，这个数列就叫做等差数列。以下是我为您整理的关于2017年高考数学必考等差数列公式的相关资料，希望对您有所帮助。

　高中数学知识点：等差数列公式

　等差数列公式an=a1+(n-1)d

　a1为首项，an为第n项的通项公式，d为公差

　前n项和公式为：Sn=na1+n(n-1)d/2

　Sn=(a1+an)n/2

　若m+n=p+q则：存在am+an=ap+aq

　若m+n=2p则：am+an=2ap

　以上n.m.p.q均为正整数

　解析：第n项的值an=首项+(项数-1)?公差

　前n项的和Sn=首项?n+项数(项数-1)公差/2

　公差d=(an-a1)?(n-1)

　项数=(末项-首项)?公差+1

　数列为奇数项时，前n项的和=中间项?项数

　数列为偶数项，求首尾项相加，用它的和除以2

　等差中项公式2an+1=an+an+2其中{an}是等差数列

　通项公式：公差?项数+首项-公差

　高中数学知识点：等差数列求和公式

　若一个等差数列的首项为a1，末项为an那么该等差数列和表达式为：

　S=(a1+an)n?2

　即(首项+末项)?项数?2

　前n项和公式

　注意：n是正整数(相当于n个等差中项之和)

　等差数列前N项求和，实际就是梯形公式的妙用：

　上底为：a1首项，下底为a1+(n-1)d，高为n。

　即[a1+a1+(n-1)d]* n/2={a1n+n(n-1)d}/2。

　高中数学知识点：推理过程

　设首项为 , 末项为 , 项数为 , 公差为 , 前 项和为 , 则有:

　当d?0时，Sn是n的二次函数，(n，Sn)是二次函数 的图象上一群孤立的点。利用其几何意义可求前n项和Sn的最值。

　注意：公式一二三事实上是等价的，在公式一中不必要求公差等于一。

　求和推导

　证明：由题意得：

　Sn=a1+a2+a3+。。。+an①

　Sn=an+a(n-1)+a(n-2)+。。。+a1②

　①+②得：

　2Sn=[a1+an]+[a2+a(n-1)]+[a3+a(n-2)]+...+[a1+an](当n为偶数时)

　Sn={[a1+an]+[a2+a(n-1)]+[a3+a(n-2)]+...+[a1+an]}/2

　Sn=n(A1+An)/2 (a1，an，可以用a1+(n-1)d这种形式表示可以发现括号里面的数都是一个定值，即(A1+An)

　基本公式

　公式　Sn=(a1+an)n/2

　等差数列求和公式

　Sn=na1+n(n-1)d/2; (d为公差)

　Sn=An2+Bn; A=d/2,B=a1-(d/2)

　和为 Sn

　首项 a1

　末项 an

　公差d

　项数n

　表示方法

　等差数列基本公式:

　末项=首项+(项数-1)?公差

　项数=(末项-首项)?公差+1

　首项=末项-(项数-1)?公差

　和=(首项+末项)?项数?2

　差:首项+项数?(项数-1)?公差?2

　说明

　末项:最后一位数

　首项:第一位数

　项数:一共有几位数

　和:求一共数的总和

　本段通项公式

　首项=2?和?项数-末项

　末项=2?和?项数-首项

　末项=首项+(项数-1)?公差:a1+(n-1)d

　项数=(末项-首项)/ 公差+1 :n=(an-a1)/d+1

　公差= d=(an-a1)/n-1

　如：1+3+5+7+?99 公差就是3-1

　将a1推广到am，则为:

　d=(an-am)/n-m

　基本性质

　若 m、n、p、q?N

　①若m+n=p+q，则am+an=ap+aq

　②若m+n=2q，则am+an=2aq(等差中项)